When Predictors Collide: Mastering VIF in Multicollinear Regression

In regression models, the independent variables must be not or only slightly dependent on each other, i.e. that they are not correlated. However, if such a dependency exists, this is referred to as Multicollinearity and leads to unstable models and results that are difficult to interpret. The variance inflation factor is a decisive metric for recognizing multicollinearity and indicates the extent to which the correlation with other predictors increases the variance of a regression coefficient. A high value of this metric indicates a high correlation of the variable with other independent variables in the model.

In the following article, we look in detail at multicollinearity and the VIF as a measurement tool. We also show how the VIF can be interpreted and what measures can be taken to reduce it. We also compare the indicator with other methods for measuring multicollinearity.

What is Multicollinearity?

Multicollinearity is a phenomenon that occurs in regression analysis when two or more variables are strongly correlated with each other so that a change in one variable leads to a change in the other variable. As a result, the development of an independent variable can be predicted completely or at least partially by another variable. This complicates the prediction of linear regression to determine the influence of an independent variable on the dependent variable.

A distinction can be made between two types of multicollinearity:

• Perfect Multicollinearity: a variable is an exact linear combination of another variable, for example when two variables measure the same thing in different units, such as weight in kilograms and pounds.
• High Degree of Multicollinearity: Here, one variable is strongly, but not completely, explained by at least one other variable. For example, there is a high correlation between a person’s education and their income, but it is not perfect multicollinearity.

The occurrence of multicollinearity in regressions leads to serious problems as, for example, the regression coefficients become unstable and react very strongly to new data, so that the overall prediction quality suffers. Various methods can be used to recognize multicollinearity, such as the correlation matrix or the variance inflation factor, which we will look at in more detail in the next section.

What is the Variance Inflation Factor (VIF)?

The variance inflation factor (VIF) describes a diagnostic tool for regression models that helps to detect multicollinearity. It indicates the factor by which the variance of a coefficient increases due to the correlation with other variables. A high VIF value indicates a strong multicollinearity of the variable with other independent variables. This negatively influences the regression coefficient estimate and results in high standard errors. It is therefore important to calculate the VIF so that multicollinearity is recognized at an early stage and countermeasures can be taken. The VIF for a single variable (i) is calculated using this formula:

[] [VIF = frac{1}{(1 – R^2)}]

Here (R^2) is the so-called coefficient of determination of the regression of feature (i) against all other independent variables. A high (R^2) value indicates that a large proportion of the variables can be explained by the other features, so that multicollinearity is suspected.

In a regression with the three independent variables (X_1), (X_2) and (X_3), for example, one would train a regression with (X_1) as the dependent variable and (X_2) and (X_3) as independent variables. With the help of this model, (R_{1}^2) could then be calculated and inserted into the formula for the VIF. This procedure would then be repeated for the remaining combinations of the three independent variables.

A typical threshold value is VIF > 10, which indicates strong multicollinearity. In the following section, we look in more detail at the interpretation of the variance inflation factor.

How can different Values of the Variance Inflation Factor be interpreted?

After calculating the VIF, it is important to be able to evaluate what statement the value makes about the situation in the model and to be able to deduce whether measures are necessary. The values can be interpreted as follows:

• VIF = 1: This value indicates that there is no multicollinearity between the analyzed variable and the other variables. This means that no further action is required.
• VIF between 1 and 5: If the value is in the range between 1 and 5, then there is multicollinearity between the variables, but this is not large enough to represent an actual problem. Rather, the dependency is still moderate enough that it can be absorbed by the model itself.
• VIF > 5: In such a case, there is already a high degree of multicollinearity, which requires intervention in any case. The standard error of the predictor is likely to be significantly excessive, so the regression coefficient may be unreliable. Consideration should be given to combining the correlated predictors into one variable.
• VIF > 10: With such a value, the variable has serious multicollinearity and the regression model is very likely to be unstable. In this case, consideration should be given to removing the variable to obtain a more powerful model.

Overall, a high VIF value indicates that the variable may be redundant, as it is highly correlated with other variables. In such cases, various measures should be taken to reduce multicollinearity.

What measures help to reduce the VIF?

There are various ways to circumvent the effects of multicollinearity and thus also reduce the variance inflation factor. The most popular measures include:

• Removing highly correlated variables: Especially with a high VIF value, removing individual variables with high multicollinearity is a good tool. This can improve the results of the regression, as redundant variables estimate the coefficients more unstable.
• Principal component analysis (PCA): The core idea of principal component analysis is that several variables in a data set may measure the same thing, i.e. be correlated. This means that the various dimensions can be combined into fewer so-called principal components without compromising the significance of the data set. Height, for example, is highly correlated with shoe size, as tall people often have taller shoes and vice versa. This means that the correlated variables are then combined into uncorrelated main components, which reduces multicollinearity without losing important information. However, this is also accompanied by a loss of interpretability, as the principal components do not represent real characteristics, but a combination of different variables.
• Regularization Methods: Regularization comprises various methods that are used in statistics and machine learning to control the complexity of a model. It helps to react robustly to new and unseen data and thus enables the generalizability of the model. This is achieved by adding a penalty term to the model’s optimization function to prevent the model from adapting too much to the training data. This approach reduces the influence of highly correlated variables and lowers the VIF. At the same time, however, the accuracy of the model is not affected.

These methods can be used to effectively reduce the VIF and combat multicollinearity in a regression. This makes the results of the model more stable and the standard error can be better controlled.

How does the VIF compare to other methods?

The variance inflation factor is a widely used technique to measure multicollinearity in a data set. However, other methods can offer specific advantages and disadvantages compared to the VIF, depending on the application.

Correlation Matrix

The correlation matrix is a statistical method for quantifying and comparing the relationships between different variables in a data set. The pairwise correlations between all combinations of two variables are shown in a tabular structure. Each cell in the matrix contains the so-called correlation coefficient between the two variables defined in the column and the row.

This value can be between -1 and 1 and provides information on how the two variables relate to each other. A positive value indicates a positive correlation, meaning that an increase in one variable leads to an increase in the other variable. The exact value of the correlation coefficient provides information on how strongly the variables move about each other. With a negative correlation coefficient, the variables move in opposite directions, meaning that an increase in one variable leads to a decrease in the other variable. Finally, a coefficient of 0 indicates that there is no correlation.

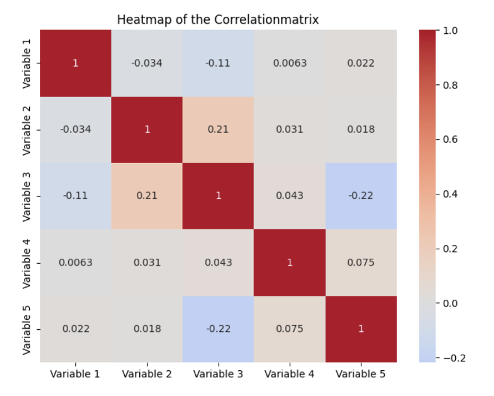
A correlation matrix therefore fulfills the purpose of presenting the correlations in a data set in a quick and easy-to-understand way and thus forms the basis for subsequent steps, such as model selection. This makes it possible, for example, to recognize multicollinearity, which can cause problems with regression models, as the parameters to be learned are distorted.

Compared to the VIF, the correlation matrix only offers a surface analysis of the correlations between variables. However, the biggest difference is that the correlation matrix only shows the pairwise comparisons between variables and not the simultaneous effects between several variables. In addition, the VIF is more useful for quantifying exactly how much multicollinearity affects the estimate of the coefficients.

Eigenvalue Decomposition

Eigenvalue decomposition is a method that builds on the correlation matrix and mathematically helps to identify multicollinearity. Either the correlation matrix or the covariance matrix can be used. In general, small eigenvalues indicate a stronger, linear dependency between the variables and are therefore a sign of multicollinearity.

Compared to the VIF, the eigenvalue decomposition offers a deeper mathematical analysis and can in some cases also help to detect multicollinearity that would have remained hidden by the VIF. However, this method is much more complex and difficult to interpret.

The VIF is a simple and easy-to-understand method for detecting multicollinearity. Compared to other methods, it performs well because it allows a precise and direct analysis that is at the level of the individual variables.

How to detect Multicollinearity in Python?

Recognizing multicollinearity is a crucial step in data preprocessing in machine learning to train a model that is as meaningful and robust as possible. In this section, we therefore take a closer look at how the VIF can be calculated in Python and how the correlation matrix is created.

Calculating the Variance Inflation Factor in Python

The Variance Inflation Factor can be easily used and imported in Python via the statsmodels library. Assuming we already have a Pandas DataFrame in a variable X that contains the independent variables, we can simply create a new, empty DataFrame for calculating the VIFs. The variable names and values are then saved in this frame.

A new row is created for each independent variable in X in the Variable column. It is then iterated through all variables in the data set and the variance inflation factor is calculated for the values of the variables and again saved in a list. This list is then stored as column VIF in the DataFrame.

Calculating the Correlation Matrix

In Python, a correlation matrix can be easily calculated using Pandas and then visualized as a heatmap using Seaborn. To illustrate this, we generate random data using NumPy and store it in a DataFrame. As soon as the data is stored in a DataFrame, the correlation matrix can be created using the corr() function.

If no parameters are defined within the function, the Pearson coefficient is used by default to calculate the correlation matrix. Otherwise, you can also define a different correlation coefficient using the method parameter.

Finally, the heatmap is visualized using seaborn. To do this, the heatmap() function is called and the correlation matrix is passed. Among other things, the parameters can be used to determine whether the labels should be added and the color palette can be specified. The diagram is then displayed with the help of matplolib.

This is what you should take with you

• The variance inflation factor is a key indicator for recognizing multicollinearity in a regression model.
• The coefficient of determination of the independent variables is used for the calculation. Not only the correlation between two variables can be measured, but also combinations of variables.
• In general, a reaction should be taken if the VIF is greater than five, and appropriate measures should be introduced. For example, the affected variables can be removed from the data set or the principal component analysis can be performed.
• In Python, the VIF can be calculated directly using statsmodels. To do this, the data must be stored in a DataFrame. The correlation matrix can also be calculated using Seaborn to detect multicollinearity.

The post When Predictors Collide: Mastering VIF in Multicollinear Regression appeared first on Towards Data Science.